Masalahnya dapat diselesaikan di O (polylog (b)).
Kami mendefinisikan f(d, n)jumlah bilangan bulat hingga d angka desimal dengan jumlah digit kurang dari atau sama dengan n. Dapat dilihat bahwa fungsi ini diberikan oleh rumus

Mari kita turunkan fungsi ini, dimulai dengan sesuatu yang lebih sederhana.
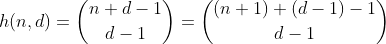
Fungsi h menghitung jumlah cara untuk memilih elemen d-1 dari multi-set yang berisi n + 1 elemen berbeda. Ini juga merupakan sejumlah cara untuk mem-partisi n menjadi d bin, yang dapat dengan mudah dilihat dengan membangun pagar d-1 di sekitar n dan menyimpulkan setiap bagian yang terpisah. Contoh untuk n = 2, d = 3 ':
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
Jadi, h menghitung semua angka yang memiliki jumlah digit n dan d. Kecuali itu hanya bekerja untuk n kurang dari 10, karena digit terbatas pada 0 - 9. Untuk memperbaikinya untuk nilai 10 - 19, kita perlu mengurangi jumlah partisi yang memiliki satu bin dengan angka lebih besar dari 9, yang akan saya sebut nampan berlebih mulai sekarang.
Istilah ini dapat dihitung dengan menggunakan kembali h dengan cara berikut. Kami menghitung jumlah cara untuk mempartisi n - 10, dan kemudian memilih salah satu nampan untuk memasukkan 10, yang menghasilkan jumlah partisi yang memiliki satu nampan berlebih. Hasilnya adalah fungsi pendahuluan berikut.
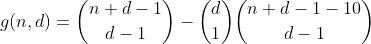
Kami melanjutkan cara ini untuk n kurang atau sama dengan 29, dengan menghitung semua cara mempartisi n - 20, lalu memilih 2 nampan tempat kami menempatkan 10, ke dalam, dengan demikian menghitung jumlah partisi yang berisi 2 nampan berlebih.
Tetapi pada titik ini kita harus berhati-hati, karena kita sudah menghitung partisi memiliki 2 nampan berlebih pada periode sebelumnya. Bukan hanya itu, tetapi sebenarnya kami menghitungnya dua kali. Mari kita gunakan contoh dan lihat partisi (10,0,11) dengan jumlah 21. Dalam istilah sebelumnya, kita kurangi 10, hitung semua partisi dari sisa 11 dan masukkan 10 ke dalam salah satu dari 3 tempat sampah. Tetapi partisi khusus ini dapat dicapai dengan satu dari dua cara:
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
Karena kami juga menghitung partisi ini sekali dalam jangka waktu pertama, jumlah total partisi dengan 2 nampan berlebih berjumlah 1 - 2 = -1, jadi kami perlu menghitungnya sekali lagi dengan menambahkan istilah berikutnya.
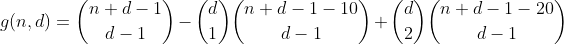
Berpikir tentang ini sedikit lebih, kami segera menemukan bahwa berapa kali sebuah partisi dengan jumlah tertentu dari tempat sampah yang berlebih dihitung dalam istilah tertentu dapat diekspresikan oleh tabel berikut ini (kolom i mewakili istilah i, baris j partisi dengan j overflown sampah).
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
Ya, itu segitiga Pascal. Satu-satunya penghitungan yang kami minati adalah yang ada di baris / kolom pertama, yaitu jumlah partisi dengan nol tempat sampah berlebih. Dan karena jumlah bolak-balik dari setiap baris tetapi yang pertama sama dengan 0 (misalnya 1 - 4 + 6 - 4 + 1 = 0), itulah cara kita menyingkirkannya dan sampai pada rumus kedua dari belakang.
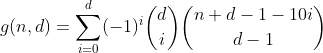
Fungsi ini menghitung semua angka dengan d digit memiliki jumlah digit n.
Sekarang, bagaimana dengan angka dengan jumlah digit kurang dari n? Kita dapat menggunakan perulangan standar untuk binomial ditambah argumen induktif, untuk menunjukkannya
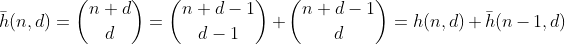
menghitung jumlah partisi dengan digit-sum paling banyak n. Dan dari sini f dapat diturunkan dengan menggunakan argumen yang sama seperti untuk g.
Dengan menggunakan rumus ini, misalnya kita dapat menemukan jumlah angka berat dalam interval dari 8000 hingga 8999 sebagai 1000 - f(3, 20) , karena ada ribuan angka dalam interval ini, dan kita harus mengurangi jumlah angka dengan jumlah digit kurang dari atau sama dengan 28 sambil memperhitungkan bahwa digit pertama sudah memberikan kontribusi 8 ke jumlah digit.
Sebagai contoh yang lebih kompleks mari kita lihat jumlah angka berat dalam interval 1234..5678. Pertama-tama kita dapat beralih dari 1234 ke 1240 dalam langkah-langkah 1. Kemudian kita beralih dari 1240 hingga 1300 dalam langkah-langkah 10. Rumus di atas memberi kita jumlah angka berat dalam setiap interval seperti itu:
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
Sekarang kita beralih dari 1300 ke 2000 dalam langkah 100:
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
Dari 2000 hingga 5000 dalam langkah 1000:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
Sekarang kita harus mengurangi ukuran langkah lagi, dari 5000 menjadi 5600 di langkah 100, dari 5600 ke 5670 di langkah 10 dan akhirnya dari 5670 menjadi 5678 di langkah 1.
Contoh implementasi Python (yang menerima sedikit optimisasi dan pengujian sementara itu):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
Sunting : Mengganti kode dengan versi yang dioptimalkan (yang terlihat lebih jelek dari kode aslinya). Juga memperbaiki beberapa kasus sudut saat saya berada di sana. heavy(1234, 100000000)membutuhkan waktu sekitar satu milidetik pada mesin saya.
