Bisakah langkah "membagi" dalam semacam penggabungan dihindari?

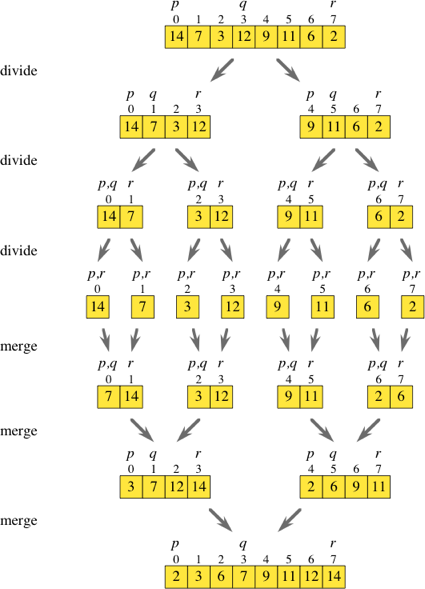
Gabungkan semacam

Jadi penggabungan sort adalah algoritma divide and conquer. Ketika saya melihat diagram di atas, saya berpikir apakah mungkin untuk mem-bypass semua langkah pembagian.

Jika Anda mengulangi lebih dari array asli sambil melompat dua, Anda bisa mendapatkan elemen di at i dan i +1 dan menempatkan mereka ke dalam array yang diurutkan sendiri. Setelah Anda memiliki semua sub-array ini ([7,14], [3,12], [9,11] dan [2,6] seperti yang ditunjukkan pada diagram), Anda dapat melanjutkan dengan rutin gabungan normal untuk mendapatkan array yang diurutkan.

Apakah iterasi melalui array dan segera menghasilkan sub-array yang diperlukan kurang efisien daripada melakukan langkah-langkah membagi secara keseluruhan?

— Jimmy_Rustle
sumber

Terkait: cs.stackexchange.com/questions/77075/…

— Omar

Jawaban:

Kebingungan muncul dari perbedaan antara deskripsi konseptual dari algoritma, dan implementasinya .

Secara logis menggabungkan semacam digambarkan sebagai memisahkan array menjadi array yang lebih kecil, dan kemudian menggabungkannya kembali bersama-sama. Namun, "pemisahan array" tidak menyiratkan "membuat array yang sama sekali baru di memori", atau apa pun seperti itu - itu dapat diimplementasikan dalam kode sebagai

/*
 * Note: array is now split into  [0..n) and [n..N)
 */

yaitu tidak ada pekerjaan yang sebenarnya terjadi, dan "pemisahan" adalah murni konseptual. Jadi apa yang Anda sarankan tentu berhasil, tetapi secara logis Anda masih "memecah" array - Anda hanya tidak memerlukan pekerjaan apa pun dari komputer untuk melakukannya :-)

— psmears
sumber

Secara pribadi saya sangat suka semacam penggabungan dari bawah ke atas karena lebih mudah untuk diterapkan dengan cara yang memungkinkan Anda menghindari mengalokasikan buffer temp pada setiap tingkat rekursi. Alih-alih Anda mengalokasikan buffer sekali dan ping-pong di antara mereka.

— ratchet freak

Pembagian - ini secara komputasional bukan pilihan ... plus saran OPs hanyalah perkenalan yang setara dengan penggabungan array elemen tunggal, dan mulai menggunakan penggabungan dari langkah ke-2, yang tampaknya berlebihan, karena penggabungan orisinal juga berfungsi. Tidak ada gunanya mengoptimalkan itu. Itu hanya memperkenalkan konsep dan logika yang berlebihan.

— luk32

@ scratchetfreak: Saya juga menyukainya, tapi sayangnya itu tidak setara dengan top-down (setidaknya versi yang saya tahu). Ini akan melakukan penggabungan berbeda, pada dasarnya membulatkan ke panjang array power-of-2 berikutnya, yang saya pikir bahkan mungkin sedikit lebih lambat. Apakah Anda tahu versi bottom-up yang melakukan penggabungan yang sama persis tanpa membayar biaya yang lumayan di tempat lain?

— user541686

@Mehrdad satu-satunya masalah sebenarnya adalah ekor kecil yang perlu digabung. Dalam kasus terburuk itu berarti lulus lain untuk bergabung dalam satu item untuk array panjang 1<<n+1. Meskipun saya yakin Anda dapat menyesuaikan hal-hal sehingga ekor yang terlalu kecil bisa digabung menjadi bagian yang lebih rendah.

— ratchet freak

@psmears "Anda hanya tidak memerlukan pekerjaan dari komputer untuk melakukannya" - jadi saya menduga biaya kinerja dari n panggilan beberapa fungsi pembagian rekursif (7 panggilan dalam diagram contoh) pada dasarnya dapat diabaikan?

— Jimmy_Rustle

Saya kira yang Anda maksud adalah implementasi bottom-up . Dalam implementasi bottom-up Anda mulai dari elemen sel tunggal bergerak ke atas dengan menggabungkan elemen ke dalam daftar / array yang lebih besar diurutkan. Balikkan panah pada gambar di atas mulai dari array tengah, yaitu array satu elemen.

Selain itu, Anda mungkin ingin mengoptimalkan penggabungan dengan membagi array hingga mencapai ukuran konstan, setelah itu Anda cukup mengurutkannya menggunakan misalnya penyisipan misalnya.

Kalau tidak, menyortir tanpa memisahkan array tidak mungkin. Sebenarnya inti dari jenis Gabung adalah membagi dan menyortir subarrays, yaitu, membagi-dan-taklukkan.

— fade2black
sumber