Mengapa anil kuantum tidak dapat dijelaskan oleh model gerbang?

Ini adalah pertanyaan yang saya terinspirasi untuk bertanya berdasarkan pertanyaan ini , yang mencatat bahwa anil kuantum adalah model yang sama sekali berbeda untuk perhitungan daripada model rangkaian biasa. Saya pernah mendengar ini sebelumnya, dan ini adalah pemahaman saya bahwa model gerbang tidak berlaku untuk kuantum-anil, tetapi saya tidak pernah benar-benar mengerti mengapa itu, atau bagaimana menguraikan perhitungan yang dapat dilakukan oleh seorang annealer. Seperti yang saya pahami dari beberapa pembicaraan (beberapa oleh D-wave sendiri!) Fakta bahwa para annealer terbatas pada permainan khusus Hamiltonian di dalamnya.

Quantum Annealer, seperti mesin D-Wave adalah representasi fisik dari model Ising dan karena itu memiliki 'masalah' Hamiltonian dalam bentuk

Pada dasarnya, masalah yang harus dipecahkan dipetakan ke Hamiltonian di atas. Sistem dimulai dengan Hamiltonian dan parameter annealing, digunakan untuk memetakan Hamiltonian awal ke masalah Hamiltonian menggunakan .$H_I = \sum_{J=1}^nh'_j\sigma_j^x$$s$$H_I$$H_P$$H\left(s\right) = \left(1-s\right)H_I + sH_P$

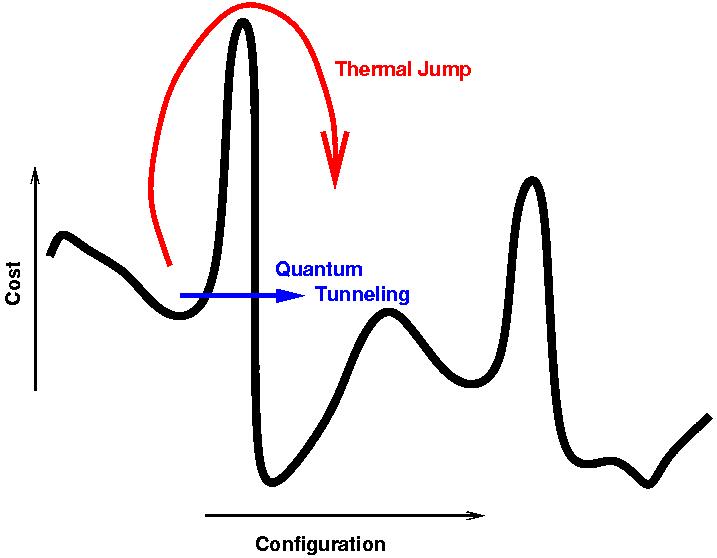
Karena ini adalah anil, proses dilakukan cukup lambat untuk tetap berada di dekat kondisi dasar sistem sedangkan Hamiltonian bervariasi dengan masalah, menggunakan tunneling untuk tetap di dekat kondisi dasar seperti yang dijelaskan dalam jawaban Nat .

Sekarang, mengapa ini tidak bisa digunakan untuk menggambarkan model gerbang QC? Di atas adalah masalah Quadratic unconstrained binary optimization (QUBO) , yang merupakan NP-hard ... Memang, inilah artikel yang memetakan sejumlah masalah NP ke model Ising . Setiap masalah dalam NP dapat dipetakan ke masalah NP-hard dalam waktu polinomial dan factorisation integer memang merupakan masalah NP.

Nah, suhunya tidak nol, jadi tidak akan berada di kondisi dasar di seluruh anil dan akibatnya, solusinya masih hanya perkiraan. Atau, dalam istilah yang berbeda, probabilitas kegagalan lebih besar dari setengah (ini sama sekali tidak memiliki probabilitas keberhasilan yang layak dibandingkan dengan apa yang oleh QC universal dianggap 'layak' - dilihat dari grafik yang telah saya lihat, probabilitas keberhasilan untuk mesin saat ini sekitar dan ini hanya akan bertambah buruk dengan meningkatnya ukuran), dan algoritma anneal tidak dibatasi kesalahan. Sama sekali. Dengan demikian, tidak ada cara untuk mengetahui apakah Anda punya solusi yang tepat dengan sesuatu seperti factorisation integer.$0.2\%$

Apa yang (pada prinsipnya) lakukan adalah mendekati hasil yang tepat, sangat cepat, tetapi ini tidak membantu untuk apa pun di mana hasil yang tepat diperlukan karena beralih dari 'hampir benar' ke 'benar' masih merupakan hal yang sangat sulit ( yaitu mungkin masih NP secara umum, ketika masalah aslinya ada di NP) masalah dalam kasus ini, karena parameter yang / memberikan solusi 'hampir benar' tidak akan didistribusikan di dekat parameter yang / berikan solusi yang benar.

Edit untuk klarifikasi: artinya adalah bahwa kuantum annealer (QA) masih membutuhkan waktu eksponensial (meskipun berpotensi waktu eksponensial lebih cepat) untuk menyelesaikan masalah NP seperti factorisation bilangan bulat, di mana QC universal memberikan kecepatan eksponensial dan dapat menyelesaikan hal yang sama masalah dalam waktu poli. Inilah yang menyiratkan QA tidak dapat mensimulasikan QC universal dalam waktu poli (jika tidak dapat memecahkan masalah dalam waktu poli itu tidak bisa). Seperti yang ditunjukkan dalam komentar, ini tidak sama dengan mengatakan bahwa QA tidak dapat memberikan peningkatan yang sama dalam masalah lain, seperti pencarian basis data.

Annealing lebih merupakan taktik analog.

Intinya adalah Anda memiliki beberapa fungsi aneh yang ingin Anda optimalkan. Jadi, Anda bangkit di sekitarnya. Pada awalnya, " suhu " sangat tinggi, sehingga titik yang dipilih dapat memantul banyak. Kemudian ketika algoritma " dingin ", suhu turun, dan memantul menjadi kurang agresif.

Pada akhirnya, ia menetap pada optima lokal yang, idealnya, lebih disukai seperti optima global.

Berikut ini adalah animasi untuk anil simulasi (non-kuantum):

Tapi, itu konsep yang hampir sama untuk anil kuantum :

Sebaliknya, gerbang-logika jauh lebih digital daripada analog. Ini berkaitan dengan qubit dan operasi logis daripada hanya menemukan hasil setelah kekacauan memantul.