Bagaimana cara berpikir tentang gerbang Z di bola Bloch?

10

Saya bingung tentang cara memahami gerbang $Z$ di bola Bloch.

Mempertimbangkan matriks dapat dimengerti bahwa dan . $Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$ $Z|0\rangle = |0\rangle$ $Z|1\rangle = -|1\rangle$

Dijelaskan di sini bahwa gerbang adalah rotasi di sekitar sumbuLalu, bagaimana saya harus mengerti ? Karena adalah kutub selatan, saya merasa wajar untuk berpikir bahwa rotasi di sekitar sumbu tidak melakukan apa-apa. $Z$ $\pi$ $Z$ $Z|1\rangle = -|1\rangle$ $|1\rangle$ $\pi$ $Z$

quantum-gate bloch-sphere

— Bick
sumber

7

Cara untuk berpikir tentang bola Bloch adalah dalam hal matriks kepadatan untuk negara. bertindak padaatautidak melakukan apa-apa, seperti yang berlaku untuk matriks kerapatan diagonal. Untuk melihat efek rotasi, Anda perlu melihat bagaimana setiap matriks kepadatan non-diagonal diubah oleh , seperti. $Z$ $|0\rangle\langle 0|$ $|1\rangle\langle 1|$ $Z$ $|+\rangle\langle +|$

— DaftWullie
sumber

7

dan ditugaskan ke titik yang sama pada bola Bloch karena mereka samahingga fase global yang. Secara aljabar: mana berarti "sama hingga fase global". Berarti ada beberapa sedemikian rupa sehingga . $|1\rangle$ $-|1\rangle$ $|1\rangle \equiv -|1\rangle$ $\equiv$ $\theta$ $-|1\rangle = e^{i \theta} |1\rangle$

Hal yang membingungkan Anda adalah bahwa, terlepas dari kenyataan bahwa dan , ini tidak benar untuk kombinasi linear dari dua. Misalnya, Meskipun $|0\rangle \equiv Z |0\rangle$ $|1\rangle \equiv Z |1\rangle$ $Z |+\rangle \not\equiv Z |+\rangle$ . $|+\rangle = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$

— Craig Gidney
sumber

2

Sesuai Wikipedia , kami dapat menulis status murni apa pun sebagai

| ψ ⟩ = \cos (\frac{θ}{2}) | 0 ⟩ + e^{i ϕ} \sin (\frac{θ}{2}) | 1 ⟩

$|\psi\rangle = \cos\left( \frac{\theta}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\theta}{2} \right) |1 \rangle$

Di mana dan adalah sudut pada bola Bloch: $\theta$ $\phi$

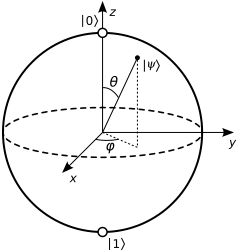
Hampir setiap titik di permukaan (yaitu keadaan murni) memiliki representasi unik dalam hal sudut, kecuali untuk kutub. Sama seperti di Bumi, Kutub Selatan tidak memiliki garis bujur yang jelas (garis bujur mana pun bekerja sama), untuk setiap negara fase berarti hal yang sama. "Lintang" ada di sini , mari kita tancapkan itu ke dalam persamaan: $|1 \rangle$ $\phi$ $\theta$ $\pi$

| 1 ⟩ = \cos (\frac{π}{2}) | 0 ⟩ + e^{i ϕ} \sin (\frac{π}{2}) | 1 ⟩ =

$|1\rangle = \cos\left( \frac{\pi}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\pi}{2} \right) |1 \rangle =$

= 0 + e^{i ϕ} | 1 ⟩

$= 0 + e^{i \phi} |1 \rangle$

Jika Anda terbiasa dengan identitas Euler, Anda mungkin akan mengenali sebagai rotasi di bidang kompleks. Secara khusus, karena adalah rotasi untuk , kita mendapatkan , akhirnya tiba di . $e^{i \phi}$ $Z$ $\phi = \pi$ $e^{i \pi} = -1$ $|1 \rangle = - |1 \rangle$

— Norrius
sumber

1

Ini salah. Menulis

menyesatkan: ini negara setara dalam bahwa mereka hanya berbeda dengan fase global, tetapi ini tidak berarti bahwa vektor negara adalah sama. Anda mendapatkan hasil itu karena Anda mengasumsikan ada suatu penambangan antara vektor-vektor negara bagian dan titik-titik pada bola Bloch, yang bukan itu masalahnya. Bijection berdiri di antara titik-titik pada bola Bloch dan negara-negara yang digambarkan sebagai matriks kepadatan

| 1 ⟩ = - | 1 ⟩

$|1\rangle=-|1\rangle$

— glS

@ GLS Terima kasih,

yang mengikuti dari itu memang mencurigakan. Apakah masuk akal untuk meningkatkan jawaban itu dari sudut pandang Anda, atau apakah itu salah?

1 = - 1

$1=-1$

— Norrius

itu adalah panggilan Anda =). Saya pikir jawaban yang tepat adalah yang diberikan oleh DaftWullie (saya percaya penanya memiliki kesalahpahaman yang sama dengan yang ada di jawaban Anda). Saya tidak melihat banyak yang tersisa untuk dikatakan tentang pertanyaan ini

— glS