Dengan asumsi variabel-variabelnya positif atau non-negatif, ujung-ujungnya hanyalah titik-titik di mana data akan menjadi 0 atau negatif. Karena data kehidupan nyata cenderung condong ke kanan, kami melihat kepadatan titik yang lebih besar di ujung bawah distribusi mereka dan karenanya kepadatan yang lebih besar di "titik" baji.
Secara lebih umum, PCA hanyalah rotasi data dan kendala pada data tersebut umumnya akan terlihat dalam komponen utama dengan cara yang sama seperti yang ditunjukkan dalam pertanyaan.
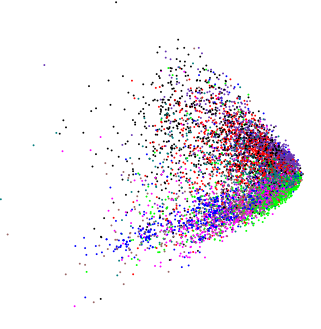
Berikut adalah contoh menggunakan beberapa variabel log-terdistribusi normal:
library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

Tergantung pada rotasi yang tersirat oleh dua PC pertama, Anda mungkin melihat irisan atau Anda mungkin melihat versi yang agak berbeda, tunjukkan di sini dalam 3d menggunakan ( ordirgl()sebagai pengganti plot())

Di sini, di 3d kita melihat beberapa paku yang menonjol dari massa tengah.
Untuk variabel acak Gaussian ( ) di mana masing-masing memiliki mean dan varians yang sama, kita melihat bola titikXi∼(N)(μ=0,σ=1)
set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")


Dan untuk variabel acak positif seragam kita melihat sebuah kubus
set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")


Perhatikan bahwa di sini, untuk ilustrasi saya menunjukkan seragam hanya menggunakan 3 variabel acak maka poin menggambarkan kubus di 3d. Dengan dimensi yang lebih tinggi / lebih banyak variabel, kita tidak dapat mewakili hypercube 5d dengan sempurna dalam 3d dan karenanya bentuk "kubus" yang berbeda agak terdistorsi. Masalah serupa mempengaruhi contoh-contoh lain yang ditunjukkan, tetapi masih mudah untuk melihat kendala dalam contoh-contoh itu.
Untuk data Anda, transformasi log variabel sebelum PCA akan menarik ekor dan merentangkan data rumpun, seperti halnya Anda mungkin menggunakan transformasi tersebut dalam regresi linier.
Bentuk lain dapat muncul di plot PCA; salah satu bentuk tersebut adalah artefak dari representasi metrik yang diawetkan dalam PCA dan dikenal sebagai tapal kuda . Untuk data dengan gradien panjang atau dominan (sampel disusun sepanjang dimensi tunggal dengan variabel meningkat dari 0 ke maksimum dan kemudian menurun lagi ke 0 sepanjang bagian data diketahui menghasilkan artefak tersebut. Pertimbangkan
ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
ylab = "Abundance", xlab = "Sites")

yang menghasilkan tapal kuda yang ekstrem, di mana titik-titik di ujung sumbu menekuk kembali ke tengah.

 .
. (kecuali dalam hal ini saya benar-benar ingin tahu apakah ada struktur internal).
(kecuali dalam hal ini saya benar-benar ingin tahu apakah ada struktur internal).






