Apa ide-ide utama, yaitu, konsep-konsep yang terkait dengan teorema Bayes ? Saya tidak meminta derivasi notasi matematika yang kompleks.
Tentang apa teorema Bayes?
Jawaban:
Teorema Bayes adalah hasil yang relatif sederhana, tetapi mendasar dari teori probabilitas yang memungkinkan untuk menghitung probabilitas kondisional tertentu. Probabilitas kondisional hanyalah probabilitas yang mencerminkan pengaruh satu peristiwa terhadap probabilitas yang lain.
Sederhananya, dalam bentuk yang paling terkenal, ia menyatakan bahwa probabilitas hipotesis yang diberikan data baru ( P (H | D) ; disebut probabilitas posterior) sama dengan persamaan berikut: probabilitas dari data yang diamati diberikan hipotesis ( P (D | H) ; disebut probabilitas bersyarat), kali probabilitas teori menjadi benar sebelum bukti baru ( P (H) ; disebut probabilitas sebelumnya H), dibagi dengan probabilitas melihat data itu, periode ( P (D ); disebut probabilitas marginal D).
Secara formal, persamaannya terlihat seperti ini:
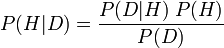
Signifikansi teorema Bayes sebagian besar karena penggunaannya yang tepat menjadi titik pertentangan antara aliran pemikiran tentang probabilitas. Bagi seorang Bayesian yang subyektif (yang mengartikan probabilitas sebagai tingkat kepercayaan subyektif) teorema Bayes memberikan landasan bagi pengujian teori, pemilihan teori dan praktik-praktik lain, dengan memasukkan penilaian probabilitas subyektif mereka ke dalam persamaan, dan berjalan dengannya. Bagi seorang frequentist (yang mengartikan probabilitas sebagai membatasi frekuensi relatif ), penggunaan teorema Bayes ini adalah penyalahgunaan, dan mereka berusaha untuk menggunakan prior (bukan-subyektif) prioror yang bermakna (seperti halnya orang Bayesia objektif di bawah interpretasi probabilitas yang lain).
Maaf, tetapi tampaknya ada beberapa kebingungan di sini: Teorema Bayes tidak cocok untuk diskusi tentang perdebatan Bayesian- Frequentist yang tidak pernah berakhir . Ini adalah teorema yang konsisten dengan kedua mazhab pemikiran (mengingat bahwa itu konsisten dengan aksioma probabilitas Kolmogorov).
Tentu saja, teorema Bayes adalah inti dari statistik Bayesian, tetapi teorema itu sendiri bersifat universal. Bentrokan antara frequentist dan Bayesian sebagian besar berkaitan dengan bagaimana distribusi sebelumnya dapat didefinisikan atau tidak.
Jadi, jika pertanyaannya adalah tentang teorema Bayes (dan bukan statistik Bayesian):
Teorema Bayes mendefinisikan bagaimana seseorang dapat menghitung probabilitas kondisional tertentu. Bayangkan misalnya Anda tahu: probabilitas seseorang memiliki gejala A, mengingat mereka memiliki penyakit Xp (A | X); probabilitas seseorang secara umum memiliki penyakit Xp (X); probabilitas seseorang secara umum memiliki gejala A p (A). dengan 3 informasi ini Anda dapat menghitung probabilitas seseorang menderita penyakit X, mengingat mereka memiliki sympotm A p (X | A).
Anda dapat memperoleh teorema Bayes sendiri sebagai berikut. Mulailah dengan definisi rasio probabilitas bersyarat:
dan hei presto:
Adapun maksudnya adalah memutar probabilitas bersyarat dengan cara ini, perhatikan contoh umum mencoba menyimpulkan kemungkinan seseorang memiliki penyakit mengingat mereka memiliki gejala, yaitu, kita tahu bahwa mereka memiliki gejala - kita hanya bisa melihatnya - tetapi kita tidak dapat memastikan apakah mereka memiliki penyakit dan harus menyimpulkannya. Saya akan mulai dengan formula dan bekerja kembali.
Jadi untuk mengatasinya, Anda perlu mengetahui probabilitas gejala sebelumnya, probabilitas penyakit sebelumnya (yaitu, seberapa umum atau jarangnya gejala dan penyakit) dan juga probabilitas bahwa seseorang memiliki gejala mengingat kita tahu seseorang memiliki gejala. suatu penyakit (misalnya, melalui tes laboratorium yang memakan waktu mahal).
Ini bisa menjadi jauh lebih rumit dari ini, misalnya, jika Anda memiliki banyak penyakit dan gejala, tetapi idenya sama. Bahkan lebih umum, teorema Bayes sering muncul jika Anda memiliki teori probabilitas hubungan antara penyebab (misalnya, penyakit) dan efek (misalnya, gejala) dan Anda perlu bernalar mundur (misalnya, Anda melihat beberapa gejala yang Anda inginkan). untuk menyimpulkan penyakit yang mendasarinya).
Ada dua aliran pemikiran utama yaitu Statistik: frequentist dan Bayesian .
Teorema Bayes berkaitan dengan yang terakhir dan dapat dilihat sebagai cara memahami bagaimana probabilitas bahwa suatu teori benar dipengaruhi oleh bukti baru. Ini dikenal sebagai probabilitas bersyarat. Anda mungkin ingin melihat ini untuk memahami matematika.
Biarkan saya memberi Anda wawasan yang sangat intuitional. Misalkan Anda melempar koin 10 kali dan Anda mendapatkan 8 kepala dan 2 ekor. Pertanyaan yang akan muncul di benak Anda adalah apakah koin ini bias terhadap kepala atau tidak.
Sekarang jika Anda menggunakan definisi konvensional atau pendekatan probabilitas yang sering Anda dapat mengatakan bahwa koin itu tidak bias dan ini adalah kejadian luar biasa. Oleh karena itu Anda akan menyimpulkan bahwa kemungkinan mendapatkan kepala berikutnya melemparkan juga 50%.
Tapi anggaplah Anda seorang Bayesian. Anda benar-benar akan berpikir bahwa karena Anda memiliki jumlah kepala yang sangat tinggi, koin memiliki bias terhadap sisi kepala. Ada beberapa metode untuk menghitung kemungkinan bias ini. Anda akan menghitungnya dan kemudian ketika Anda melempar koin itu lain kali, Anda pasti akan memanggil kepala.
Jadi, probabilitas Bayesian adalah tentang keyakinan yang Anda kembangkan berdasarkan data yang Anda amati. Saya harap itu cukup sederhana.
Teorema Bayes menghubungkan dua gagasan: probabilitas dan kemungkinan. Probabilitas mengatakan: mengingat model ini, ini adalah hasilnya. Jadi: diberi koin yang adil, saya akan mendapatkan kepala 50% dari waktu. Likelihood mengatakan: mengingat hasil ini, inilah yang dapat kita katakan tentang model. Jadi: jika Anda melemparkan koin 100 kali dan mendapatkan 88 kepala (untuk mengambil contoh sebelumnya dan membuatnya lebih ekstrem), maka kemungkinan bahwa model koin yang adil sudah benar tidak terlalu tinggi.
Salah satu contoh standar yang digunakan untuk mengilustrasikan teorema Bayes adalah ide pengujian untuk suatu penyakit: jika Anda mengikuti tes yang 95% akurat untuk penyakit yang dimiliki 1 dalam 10.000 populasi, dan Anda menguji positif, berapa kemungkinannya Anda menderita penyakit ini?
Jawaban naif adalah 95%, tetapi ini mengabaikan masalah bahwa 5% dari tes pada 9999 dari 10.000 orang akan memberikan positif palsu. Jadi kemungkinan Anda terkena penyakit ini jauh lebih rendah dari 95%.
Penggunaan frasa samar-samar saya "apa peluangnya" disengaja. Untuk menggunakan bahasa probabilitas / kemungkinan: probabilitas bahwa tes ini akurat adalah 95%, tetapi yang ingin Anda ketahui adalah kemungkinan Anda menderita penyakit tersebut.
Sedikit topik: Contoh klasik lain yang digunakan teorema Bayes untuk dipecahkan dalam semua buku pelajaran adalah masalah Monty Hall: Anda berada di acara kuis. Ada hadiah di balik salah satu dari tiga pintu. Anda memilih satu pintu. Tuan rumah membuka pintu tiga untuk mengungkapkan tidak ada hadiah. Haruskah Anda pindah ke pintu dua diberi kesempatan?
Saya suka menulis ulang pertanyaan (berdasarkan referensi di bawah): Anda berada di acara kuis. Ada hadiah di balik satu dari sejuta pintu. Anda memilih satu pintu. Tuan rumah membuka semua pintu lain kecuali pintu 104632 untuk tidak mengungkapkan hadiah. Haruskah Anda ganti ke pintu 104632?
Buku favorit saya yang membahas teorema Bayes, sangat banyak dari perspektif Bayesian, adalah "Teori Informasi, Inferensi, dan Algoritma Pembelajaran", oleh David JC MacKay. Ini buku Cambridge University Press, ISBN-13: 9780521642989. Jawaban saya adalah (saya harap) merupakan penyulingan dari jenis diskusi yang dibuat dalam buku ini. (Aturan umum berlaku: Saya tidak memiliki afiliasi dengan penulis, saya hanya suka buku).
Teorema Bayes dalam bentuknya yang paling jelas hanyalah pernyataan ulang dari dua hal:
Jadi dengan menggunakan simetri:
Jadi ini dia? Bagaimana bisa sesuatu yang begitu sederhana menjadi begitu mengagumkan? Seperti kebanyakan hal "itu perjalanan yang lebih penting daripada tujuan". Teorema bayes mengguncang karena argumen yang mengarah padanya.
Sekarang "aturan" dalam logika deduktif adalah bahwa jika Anda memiliki hubungan "A menyiratkan B" maka Anda juga memiliki "Tidak B menyiratkan Bukan A". Jadi kita memiliki "penalaran yang konsisten menyiratkan teorema Bayes". Ini berarti "teorema Tidak Bayes menyiratkan penalaran Tidak konsisten". yaitu jika hasil Anda tidak setara dengan hasil Bayesian untuk beberapa sebelum dan kemungkinan maka Anda beralasan tidak konsisten.
Hasil ini disebut teorema Cox dan dibuktikan dalam "Aljabar Kemungkinan inferensi" pada tahun 1940-an. Derivasi yang lebih baru diberikan dalam teori Proabilitas: Logika sains.
Saya sangat suka intro Kevin Murphy ke Bayes Theorem http://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html
Kutipan di sini berasal dari artikel ekonom:
http://www.cs.ubc.ca/~murphyk/Bayes/economist.html
Inti dari pendekatan Bayesian adalah untuk memberikan aturan matematis yang menjelaskan bagaimana Anda harus mengubah keyakinan Anda saat ini dengan adanya bukti baru. Dengan kata lain, ini memungkinkan para ilmuwan untuk menggabungkan data baru dengan pengetahuan atau keahlian yang ada. Contoh kanonik adalah membayangkan bahwa bayi yang baru lahir dewasa sebelum waktunya mengamati matahari terbenam pertamanya, dan bertanya-tanya apakah matahari akan naik lagi atau tidak. Dia menetapkan probabilitas sebelumnya yang sama untuk kedua hasil yang mungkin, dan mewakili ini dengan menempatkan satu marmer putih dan satu hitam ke dalam tas. Keesokan harinya, ketika matahari terbit, anak itu meletakkan marmer putih lain di dalam tas. Kemungkinan bahwa marmer yang diambil secara acak dari tas akan berwarna putih (yaitu, tingkat kepercayaan anak terhadap matahari terbit di masa depan) telah berubah dari setengah menjadi dua pertiga. Setelah matahari terbit keesokan harinya, anak itu menambahkan marmer putih lainnya, dan probabilitas (dan dengan demikian tingkat kepercayaannya) berubah dari dua pertiga menjadi tiga perempat. Dan seterusnya. Perlahan-lahan, kepercayaan awal bahwa matahari tidak mungkin terbit setiap pagi dimodifikasi menjadi hampir pasti bahwa matahari akan selalu terbit.