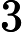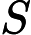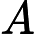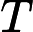Saya mengambil kursus kompleksitas dan saya mengalami masalah dengan datangnya pengurangan antara masalah NPC. Bagaimana saya bisa menemukan pengurangan di antara masalah? Apakah ada trik umum yang bisa saya gunakan? Bagaimana saya harus mendekati masalah yang meminta saya untuk membuktikan masalah adalah NPC?
Bagaimana cara membuat reduksi di antara masalah untuk membuktikan masalah adalah NP-complete?
Jawaban:
Tidak ada peluru ajaib; Bukti NP-hardness sulit. Namun, ada kerangka umum untuk semua bukti tersebut. Banyak siswa yang berjuang dengan bukti kekerasan NP bingung tentang apa yang seharusnya mereka lakukan, yang jelas membuat tidak mungkin untuk mengetahui bagaimana melakukannya. Jadi di sini adalah apa yang harus dilakukan untuk membuktikan masalah NP-hard.
Pertama, kecuali Anda hanya mengerjakan pekerjaan rumah, Anda harus memutuskan masalah NP-hard mana yang harus dikurangi menjadi masalah Anda . Ini sebagian besar adalah pertanyaan tentang "bau". Jika jumlah 3 muncul di mana saja di pernyataan masalah, cobalah mengurangi dari atau 3 C o l o r atau 3 P a r t i t i o n . (Ya, saya serius.) Jika masalah Anda melibatkan menemukan urutan atau permutasi atau jalur yang optimal, coba kurangi dari H a m i l t o n i a atau H a m i l t o n i a n P a t h . Jika masalah Anda meminta subset terkecil dengan properti tertentu, coba C l i q u e ; jika meminta untuk subset terbesar dengan properti tertentu, coba saya n d e p e n d e n t S e t . Jika masalah Anda melibatkan melakukan sesuatu di pesawat, cobalah P atau P l a n a r T S P . Dan seterusnya. Jika masalah Anda tidak "berbau" seperti apa pun, 3 S A T atau C i r c u i t S A T mungkin merupakan taruhan terbaik Anda.
Jelas, Anda harus sudah tahu persis bagaimana semua masalah ini didefinisikan , dan semakin sederhana masalah yang Anda kurangi, semakin baik. Jadi sekeren hasilnya pada akhirnya, saya tidak merekomendasikan pengurangan dari atau atau atau .
Kedua, reduksi aktual. Untuk mengurangi masalah X (yang Anda tahu adalah NP-hard) ke masalah Y (yang Anda coba buktikan adalah NP-hard, Anda perlu menjelaskan algoritma yang mengubah instance X sewenang - wenang menjadi instance legal Y Algoritma reduksi perlu melakukan sesuatu yang spesifik dengan setiap "fitur" dari instance-X; porsi output untuk setiap "fitur" biasanya disebut gadget .
Tapi apa itu fitur? Itu tergantung pada masalah X. Misalnya:
Untuk mengubah instance dari , Anda akan memerlukan gadget untuk setiap variabel dan untuk setiap klausa dalam formula input. Setiap gadget variabel harus memiliki dua "status" yang sesuai dengan "benar" dan "salah". Setiap gadget klausa juga harus memiliki beberapa "status", yang masing-masingnya entah bagaimana memaksa setidaknya satu literal dalam klausa itu menjadi benar. (Status bukan bagian dari output dari algoritma reduksi.)
Untuk mengubah instance , Anda akan memerlukan gadget untuk setiap titik dan setiap tepi grafik input, dan gadget lain untuk menentukan tiga warna.
Untuk mengubah sebuah contoh dari , Anda akan memerlukan gadget untuk setiap masukan, untuk masing-masing kawat, dan untuk setiap gerbang di sirkuit masukan.
Bentuk sebenarnya dari gadget tergantung pada masalah Y, yang Anda mengurangi ke . Misalnya, jika Anda mereduksi masalah tentang grafik, gadget Anda akan menjadi subgraph kecil; lihat artikel Wikipedia. Jika Anda mengurangi masalah tentang penjadwalan, setiap gadget akan menjadi satu set pekerjaan yang dijadwalkan. Jika Anda mengurangi masalah tentang Mario , setiap gadget akan menjadi satu set balok dan batu bata dan Koopa.
Ini bisa membingungkan jika kedua masalah melibatkan jenis objek yang sama. Misalnya, jika X dan Y merupakan masalah tentang grafik, algoritme Anda akan mengubah satu grafik (turunan X) menjadi grafik yang berbeda (turunan Y). Pilih notasi Anda dengan bijak, sehingga Anda tidak membingungkan kedua grafik ini. Saya juga sangat menyarankan menggunakan beberapa warna tinta.
Akhirnya, algoritma reduksi Anda harus memenuhi tiga properti:
Ini berjalan dalam waktu polinomial. (Ini biasanya mudah.)
Jika algoritma reduksi Anda diberi instance X positif sebagai input, ia menghasilkan instance Y positif sebagai output.
Jika algoritma reduksi Anda menghasilkan instance positif dari Y sebagai output, itu harus diberikan instance positif dari X sebagai input.
Ada kehalusan penting di sini. Algoritma reduksi Anda hanya berfungsi dalam satu arah, dari instance X ke instance Y, tetapi membuktikan algoritma yang benar memerlukan alasan tentang transformasi di kedua arah. Anda juga harus ingat bahwa algoritma reduksi Anda tidak dapat memastikan apakah instance X yang diberikan adalah positif atau negatif — yang akan membutuhkan penyelesaian masalah NP-hard dalam waktu polinomial!
Itu apa . The bagaimana hanya datang dengan praktek.
JeffE menguraikan strategi yang paling umum: tahu banyak masalah NP-complete, temukan satu yang sangat cocok dan lakukan pengurangan yang mudah .
Strategi lain yang valid adalah selalu menggunakan 3SAT (atau masalah lainnya). Ini mungkin membuat beberapa pengurangan lebih rumit, tetapi keuntungannya adalah Anda memiliki banyak pengalaman dalam mengekspresikan kepuasan dalam jenis masalah lainnya. Jadi, Anda menghemat waktu untuk menemukan mitra reduksi yang baik (termasuk jalan buntu) dan berharap pengalaman Anda akan memungkinkan Anda melakukan pengurangan dengan cepat bahkan jika itu lebih sulit.
Pendekatan ini memiliki beberapa meta beauty, juga: (3) SAT adalah salah satu dari beberapa masalah yang NP-kelengkapannya telah terbukti (hampir) secara langsung. Karena itu, hanya mengandalkan bukti yang membuat "pohon bukti" Anda tetap datar, menghindari rantai panjang pengurangan.