Mengapa tidak membuang saja jaringan saraf dan pembelajaran mendalam? [Tutup]

Masalah mendasar dengan pembelajaran mendalam dan jaringan saraf pada umumnya.

1. Solusi yang sesuai dengan data pelatihan tidak terbatas. Kami tidak memiliki persamaan matematis yang tepat yang hanya dipenuhi oleh satu saja dan dapat kami katakan sebagai generalisasi terbaik. Sederhananya kita tidak tahu mana yang paling umum.

2. Mengoptimalkan bobot bukanlah masalah cembung, jadi kita tidak pernah tahu bahwa kita berakhir dengan global atau minimum lokal.

Jadi mengapa tidak membuang saja jaringan saraf dan mencari model ML yang lebih baik? Sesuatu yang kita pahami, dan sesuatu yang konsisten dengan seperangkat persamaan matematika? Linear dan SVM tidak memiliki kekurangan matematika ini dan sepenuhnya konsisten dengan seperangkat persamaan matematika. Mengapa tidak berpikir pada jalur yang sama (tidak perlu linier) dan menghasilkan model ML baru yang lebih baik daripada Linear dan SVM serta jaringan saraf dan pembelajaran yang mendalam?

1. Tidak dapat mengetahui solusi apa yang paling umum adalah masalah, tetapi seharusnya tidak menghalangi kita untuk menggunakan solusi yang baik. Manusia sendiri sering tidak tahu apa yang menggeneralisasi terbaik (pertimbangkan, misalnya, teori fisika yang saling bersaing), tetapi itu tidak menyebabkan kita terlalu banyak masalah.

2. Telah terbukti bahwa sangat jarang pelatihan gagal karena minimum lokal. Sebagian besar minimum lokal dalam jaringan saraf dalam dekat nilainya dengan minimum global, jadi ini bukan masalah. sumber

Tetapi jawaban yang lebih luas adalah bahwa Anda dapat berbicara sepanjang hari tentang ketidaksesuaian dan pemilihan model, dan orang-orang masih akan menggunakan jaringan saraf hanya karena mereka bekerja lebih baik daripada yang lain (setidaknya pada hal-hal seperti klasifikasi gambar).

Tentu saja ada juga orang yang berargumen bahwa kita tidak boleh terlalu fokus pada CNN seperti komunitas fokus pada SVM beberapa dekade lalu, dan bukannya terus mencari hal besar berikutnya. Secara khusus, saya pikir saya ingat Hinton menyesali keefektifan CNN sebagai sesuatu yang mungkin menghambat penelitian. pos terkait

Seperti yang ditunjukkan oleh komentar pada pertanyaan Anda, ada banyak orang yang berupaya menemukan sesuatu yang lebih baik. Saya ingin menjawab pertanyaan ini dengan memperluas komentar yang ditinggalkan oleh @josh

Semua model salah tetapi ada pula yang berguna (Wiki)

Pernyataan di atas adalah kebenaran umum yang digunakan untuk menggambarkan sifat model statistik. Dengan menggunakan data yang kami miliki, kami dapat membuat model yang memungkinkan kami melakukan hal-hal berguna seperti perkiraan nilai yang diprediksi.

Ambil contoh Regresi Linier

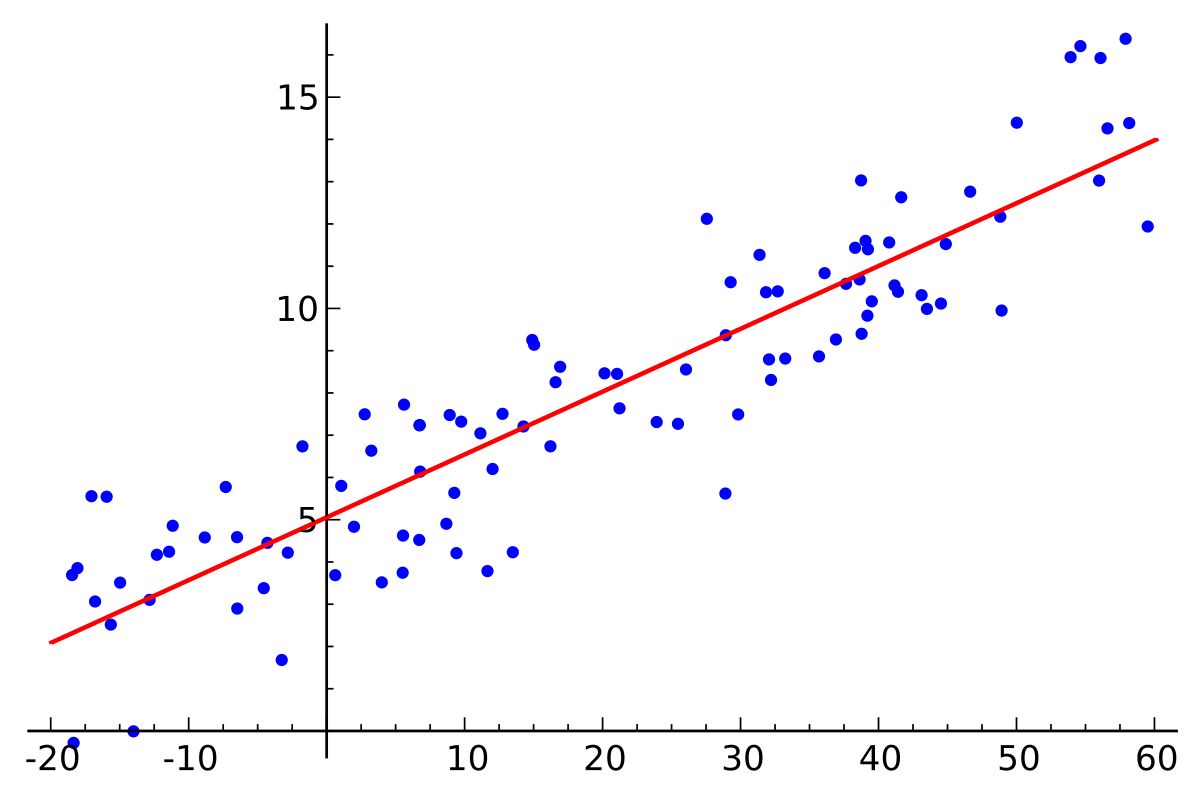
Dengan menggunakan sejumlah pengamatan, kita dapat menyesuaikan suatu model untuk memberi kita nilai perkiraan untuk variabel dependen yang memberikan nilai apa pun untuk variabel independen.

Burnham, KP; Anderson, DR (2002), Pemilihan Model dan Multimodel> Inferensi: Pendekatan Informasi-Teoretis Praktis (edisi kedua):

"Sebuah model adalah penyederhanaan atau perkiraan realitas dan karenanya tidak akan mencerminkan semua kenyataan. ... Box mencatat bahwa" semua model salah, tetapi beberapa berguna. "Sementara model tidak pernah bisa menjadi" kebenaran, "sebuah model mungkin peringkat dari sangat berguna, berguna, agak berguna untuk, akhirnya, pada dasarnya tidak berguna. "

Penyimpangan dari model kami (seperti yang dapat dilihat pada gambar di atas) tampak acak, beberapa pengamatan di bawah garis dan beberapa di atas, tetapi garis regresi kami menunjukkan korelasi umum. Sementara penyimpangan dalam model kami tampak acak, dalam skenario realistis akan ada faktor lain yang berperan yang menyebabkan penyimpangan ini. Sebagai contoh, bayangkan menonton mobil ketika mereka melewati persimpangan di mana mereka harus berbelok ke kiri atau ke kanan untuk melanjutkan, mobil-mobil berbelok tanpa pola tertentu. Sementara kita dapat mengatakan bahwa arah belokan mobil benar-benar acak, apakah setiap pengemudi mencapai persimpangan dan pada saat itu membuat keputusan acak ke arah mana untuk berbelok? Pada kenyataannya mereka mungkin menuju ke suatu tempat tertentu karena alasan tertentu, dan tanpa berusaha menghentikan setiap mobil untuk menanyakan alasan mereka, kita hanya dapat menggambarkan tindakan mereka secara acak.

Di mana kita dapat menyesuaikan model dengan deviasi minimal, seberapa yakinkah kita bahwa variabel yang tidak diketahui, tidak diketahui atau tak terukur pada suatu saat melempar model kita? Apakah kepakan sayap kupu-kupu di Brasil memicu tornado di Texas?

Masalah dengan menggunakan model Linear dan SVN yang Anda sebutkan sendiri adalah bahwa kami agak diminta untuk mengamati variabel kami secara manual dan bagaimana masing-masing memengaruhi satu sama lain. Kita kemudian perlu memutuskan variabel apa yang penting dan menulis algoritma tugas khusus. Ini bisa langsung jika kita hanya memiliki beberapa variabel, tetapi bagaimana jika kita memiliki ribuan? Bagaimana jika kita ingin membuat model pengenalan gambar umum, dapatkah ini dicapai secara realistis dengan pendekatan ini?

Pembelajaran Jauh dan Jaringan Saraf Tiruan (JST) dapat membantu kami membuat model yang berguna untuk kumpulan data besar yang berisi variabel dalam jumlah sangat besar (mis. Pustaka gambar). Seperti yang Anda sebutkan, ada sejumlah solusi yang tidak dapat dipahami yang dapat cocok dengan data menggunakan JST, tetapi apakah angka ini benar-benar berbeda dengan jumlah solusi yang perlu kita kembangkan melalui trial and error?

Aplikasi JST melakukan banyak pekerjaan untuk kita, kita dapat menentukan input dan output yang kita inginkan (dan mengubahnya kemudian untuk melakukan perbaikan) dan menyerahkannya kepada JST untuk mencari solusinya. Inilah sebabnya mengapa JST sering digambarkan sebagai "kotak hitam" . Dari input yang diberikan mereka menghasilkan perkiraan, namun (secara umum) perkiraan ini tidak termasuk rincian tentang bagaimana mereka diperkirakan.

Dan itu benar-benar turun ke masalah apa yang Anda coba selesaikan, karena masalahnya akan menentukan pendekatan model apa yang lebih berguna. Model tidak sepenuhnya akurat sehingga selalu ada unsur 'salah', namun semakin akurat hasil Anda, semakin berguna model itu. Memiliki lebih banyak detail dalam hasil tentang bagaimana perkiraan itu dibuat mungkin juga berguna, tergantung pada masalahnya bahkan mungkin lebih berguna daripada peningkatan akurasi.

Jika misalnya Anda menghitung skor kredit seseorang, menggunakan regresi dan SVM memberikan perhitungan yang dapat dieksplorasi lebih baik. Mampu men-tweak model secara langsung dan menjelaskan kepada pelanggan pengaruh variabel independen terpisah terhadap skor keseluruhan mereka sangat berguna. ANN dapat membantu dalam memproses jumlah variabel yang lebih besar untuk mencapai skor yang lebih akurat, tetapi apakah akurasi ini lebih berguna?

Minimum global mungkin juga tidak berguna, jadi kami tidak terlalu peduli apakah kami menemukannya atau tidak. Alasannya adalah, untuk jaringan yang dalam, tidak hanya waktu untuk menemukannya menjadi lebih lama secara eksponensial ketika ukuran jaringan meningkat, tetapi juga minimum global sering kali berhubungan dengan overfitting set pelatihan. Dengan demikian kemampuan generalisasi DNN (yang benar-benar kita pedulikan) akan menderita. Juga, sering kita lebih suka minima yang lebih rata sesuai dengan nilai yang lebih tinggi dari fungsi kerugian, daripada minima yang lebih tajam yang sesuai dengan nilai yang lebih rendah dari fungsi kerugian, karena yang kedua akan berurusan dengan sangat buruk dengan ketidakpastian dalam input. Ini menjadi semakin jelas dengan perkembangan Bayesian Deep Learning. Robust Optimization mengalahkan Determinist Optimization sangat sering, ketika diterapkan pada masalah dunia nyata di mana ketidakpastian itu penting.

Akhirnya, itu fakta bahwa DNNs hanya menendang keledai metode seperti XGBoost di klasifikasi gambar dan NLP. Sebuah perusahaan yang harus mengambil untung dari klasifikasi gambar akan memilihnya dengan benar sebagai model yang akan digunakan dalam produksi ( dan menginvestasikan sejumlah besar uang pada rekayasa fitur, pipa data, dll. Tetapi saya ngelantur). Ini tidak berarti bahwa mereka mendominasi semua lingkungan ML: misalnya, mereka melakukan lebih buruk daripada XGBoost pada data terstruktur (lihat pemenang terakhir kompetisi Kaggle) dan mereka tampaknya masih tidak melakukan serta filter partikel pada pemodelan seri waktu. Namun, beberapa inovasi terbaru tentang RNN dapat mengubah situasi ini.

Saya pikir cara terbaik untuk memikirkan pertanyaan ini adalah melalui pasar yang kompetitif. Jika Anda membuang pembelajaran mendalam, dan pesaing Anda menggunakannya, DAN itu terjadi bekerja lebih baik daripada apa yang Anda gunakan, maka Anda akan dikalahkan di pasar.

Saya pikir itulah yang terjadi, sebagian, hari ini, yaitu pembelajaran mendalam tampaknya bekerja lebih baik daripada apa pun untuk seluruh masalah di pasar. Misalnya, penerjemah bahasa online yang menggunakan pembelajaran mendalam lebih baik daripada pendekatan linguistik murni yang digunakan sebelumnya. Hanya beberapa tahun yang lalu ini tidak terjadi, tetapi kemajuan dalam pembelajaran mendalam membawa mereka yang terbiasa dengan posisi kepemimpinan di pasar.

Saya terus mengulang "pasar" karena itulah yang mendorong lonjakan pembelajaran mendalam saat ini. Saat bisnis menemukan sesuatu yang bermanfaat, sesuatu akan menyebar luas. Bukan kita , panitia, yang memutuskan bahwa pembelajaran mendalam harus populer. Ini bisnis dan persaingan.

Bagian kedua, selain sukses ML yang sebenarnya, ada juga rasa takut ketinggalan. Banyak bisnis paranoid bahwa jika mereka kehilangan AI, mereka akan gagal sebagai bisnis. Ketakutan ini dipenuhi oleh semua rumah konsultasi, Gartners , dll., Berbisik kepada CEO bahwa mereka harus melakukan AI atau mati besok.

Tidak ada yang memaksa bisnis untuk menggunakan pembelajaran yang mendalam. IT dan R&D sangat senang dengan mainan baru. Sorak-sorai akademia, sehingga pesta ini akan berlangsung sampai musik berhenti, yaitu sampai pembelajaran yang mendalam berhenti disampaikan. Sementara itu, Anda dapat membuangnya dan mencari solusi yang lebih baik.

Ada jawaban yang sangat baik, sebagian besar menimbang dengan kegunaan DL dan JST. Tapi saya ingin menolak OP dengan cara yang lebih mendasar, karena pertanyaannya sudah menerima begitu saja inkonsistensi matematis dari jaringan saraf.

Pertama-tama, ada adalah teori matematika belakang (kebanyakan model) Neural Networks. Anda juga bisa berpendapat bahwa regresi linier tidak menyamaratakan, kecuali model yang mendasarinya adalah ... yah, linear. Dalam algoritma neural, model diasumsikan (bahkan jika tidak secara eksplisit) dan kesalahan pemasangan dihitung. Fakta bahwa algoritma dimodifikasi dengan berbagai heuristik tidak membatalkan dukungan matematika asli. BTW, optimisasi lokal juga merupakan teori yang konsisten secara matematis, apalagi bermanfaat.

Sejalan dengan ini, jika Neural Networks hanya merupakan satu kelas metode dalam seluruh kotak peralatan ilmuwan, yang merupakan garis yang memisahkan Neural Networks dari teknik lainnya? Bahkan, SVM pernah dianggap sebagai kelas NN dan mereka masih muncul di buku yang sama. Di sisi lain, NNs dapat dianggap sebagai teknik regresi (nonlinier), mungkin dengan beberapa penyederhanaan. Saya setuju dengan OP bahwa kita harus mencari algoritma yang lebih baik, beralasan, dan efisien, terlepas dari apa Anda menandainya sebagai NN atau tidak.

Saya kira untuk beberapa masalah kita kurang peduli pada ketelitian dan kesederhanaan matematis tetapi lebih untuk kegunaannya, status saat ini adalah jaringan saraf yang lebih baik dalam melakukan tugas tertentu seperti pengenalan pola dalam pemrosesan gambar.

Ada banyak hal dalam pertanyaan ini. Mari kita bahas apa yang telah Anda tulis satu per satu.

Solusi yang sesuai dengan data pelatihan tidak terbatas. Kami tidak memiliki persamaan matematis yang tepat yang hanya dipenuhi oleh satu saja dan dapat kami katakan sebagai generalisasi terbaik.

Fakta bahwa ada banyak solusi yang tak terbatas berasal dari masalah belajar menjadi masalah yang keliru sehingga tidak mungkin ada satu pun yang menggeneralisasi yang terbaik. Juga, tanpa teorema makan siang gratis, metode apa pun yang kami gunakan tidak dapat menjamin bahwa itu adalah yang terbaik di antara semua masalah pembelajaran.

Sederhananya kita tidak tahu mana yang paling umum.

Pernyataan ini tidak sepenuhnya benar. Ada teorema tentang minimalisasi risiko empiris oleh Vapnik & Chervonenkis yang menghubungkan jumlah sampel, dimensi VC dari metode pembelajaran dan kesalahan generalisasi. Perhatikan, ini hanya berlaku untuk dataset yang diberikan. Jadi diberi dataset dan prosedur pembelajaran kita tahu batas-batas pada generalisasi. Perhatikan bahwa, untuk kumpulan data yang berbeda tidak ada dan tidak dapat menjadi prosedur pembelajaran tunggal terbaik karena tidak ada teorema makan siang gratis.

Mengoptimalkan bobot bukanlah masalah cembung, jadi kita tidak pernah tahu bahwa kita berakhir dengan global atau minimum lokal. Jadi mengapa tidak membuang saja jaringan saraf dan mencari model ML yang lebih baik?

Di sini ada beberapa hal yang perlu Anda ingat. Mengoptimalkan masalah non-cembung tidak semudah masalah cembung; itu benar. Namun, kelas metode pembelajaran yang cembung terbatas (regresi linier, SVM) dan dalam praktiknya, mereka melakukan lebih buruk daripada kelas non-cembung (meningkatkan, CNNs) pada berbagai masalah. Jadi bagian yang penting adalah bahwa dalam praktiknya jaring saraf bekerja paling baik. Meskipun ada sejumlah elemen yang sangat penting yang membuat jaring saraf bekerja dengan baik:

1. Mereka dapat diterapkan pada dataset yang sangat besar karena keturunan gradien stokastik.
2. Tidak seperti SVM, kesimpulan dengan jaring yang dalam tidak tergantung pada dataset. Ini membuat jaring saraf efisien pada waktu pengujian.
3. Dengan jaring saraf dimungkinkan untuk secara langsung mengontrol kapasitas belajar mereka (pikirkan jumlah parameter) hanya dengan menambahkan lebih banyak layer atau membuatnya lebih besar. Ini penting karena untuk set data yang berbeda Anda mungkin menginginkan model yang lebih besar atau lebih kecil.

Sesuatu yang kita pahami, dan sesuatu yang konsisten dengan seperangkat persamaan matematika? Linear dan SVM tidak memiliki kekurangan matematika ini dan sepenuhnya konsisten dengan seperangkat persamaan matematika. Mengapa tidak berpikir pada jalur yang sama (tidak perlu linier) dan menghasilkan model ML baru yang lebih baik daripada Linear dan SVM serta jaringan saraf dan pembelajaran yang mendalam?

Membuang hal-hal yang berhasil karena tidak memahaminya bukanlah arah penelitian yang hebat. Di lain pihak, upaya untuk memahami mereka adalah arah penelitian yang hebat. Juga, saya tidak setuju bahwa jaringan saraf tidak konsisten dengan persamaan matematika. Mereka cukup konsisten. Kami tahu cara mengoptimalkannya dan melakukan inferensi.

Bagaimana dengan melihat jaringan saraf dari sudut pandang eksperimental? Hanya karena kami menciptakannya, bukan berarti kami wajib memahaminya secara intuitif. Atau kita tidak diizinkan bermain dengan mereka untuk memiliki pemahaman yang lebih baik tentang apa yang mereka lakukan.

Inilah beberapa pemikiran saya tentang mereka:

• Struktur: mereka adalah hierarki. Mereka seperti pohon yang berbagi input. Akar adalah input dan daun adalah lapisan keluaran. Semakin dekat layer dengan output, semakin relevan bagi mereka, semakin besar abstraksi yang dikandungnya (ini lebih banyak tentang gambar daripada piksel).
• Fungsi: mereka "bermain" dengan data, modus operandi adalah untuk bereksperimen dengan hubungan dalam neuron (bobot) sampai hal-hal "klik" (margin kesalahan dapat diterima).

Ini konsisten dengan cara kita berpikir. Bahkan konsisten dengan cara metode ilmiah beroperasi. Jadi dengan memecahkan jaringan saraf kita juga dapat memecahkan pertanyaan umum tentang apa yang dilambangkan pengetahuan.

Jangan lupa, ada banyak bidang penelitian yang menggunakan LMs, GLM, pemodelan multilevel. Akhir-akhir ini teknik Bayesian dan Hamiltonian Monte Carlo (komunitas STAN benar-benar berada di garis depan dalam hal ini) telah cukup umur dan sejumlah masalah yang diselesaikan oleh STAN sangat mudah dan tidak benar-benar membutuhkan NN atau jaring yang dalam. Penelitian Ilmu Sosial, Ekonomi Mikro adalah dua contoh (besar) dari bidang-bidang tersebut yang mengadopsi Stan dengan cepat.

Model Stan sangat "mudah dibaca". Koefisien sebenarnya memiliki interpretasi distribusi posterior dan begitu juga prediksi. Prior adalah bagian dari proses pembuatan data dan tidak perlu terkonjugasi untuk menjadi pemain (seperti gibbs). Model yang pas di stan sangat menyenangkan, sebenarnya menyetel param MCMC yang sial secara otomatis sangat baik dan memperingatkan Anda ketika eksplorasi macet dengan visualisasi yang sangat bagus.

Jika Anda belum mencobanya, Anda dapat melihat demo stan yang keren di sini ).

Pada akhirnya saya pikir orang tidak terlalu banyak membicarakan hal ini karena penelitian di bidang ini dan masalahnya tidak begitu "seksi" / "keren" seperti halnya dengan NNs.

Apa yang biasanya terjadi ketika tidak ada konsistensi matematis (minimal dalam hal ini jaringan saraf) ... ketika tidak memberikan hasil yang diinginkan, pada set tes, bos Anda akan kembali dan berkata ... Hei kenapa tidak coba Drop out (yang berbobot, lapisan mana, berapa sakit kepala Anda karena tidak ada cara matematis untuk menentukan), jadi setelah Anda mencoba dan mudah-mudahan mendapat peningkatan marjinal tetapi tidak diinginkan, bos Anda akan kembali dan berkata, mengapa tidak mencoba pembusukan berat badan (faktor apa?)? dan kemudian, mengapa Anda tidak mencoba ReLU atau aktivasi lain pada beberapa layer, dan masih tidak, mengapa tidak mencoba 'max pooling'? masih tidak, mengapa tidak mencoba batch normalisasi, masih tidak, atau setidaknya konvergensi, tetapi hasil yang tidak diinginkan, oh Anda berada di minimum lokal, coba jadwal tingkat belajar yang berbeda, hanya mengubah arsitektur jaringan? dan ulangi semua di atas dalam kombinasi yang berbeda! Simpan dalam satu lingkaran sampai Anda berhasil!

Di sisi lain, ketika Anda mencoba SVM yang konsisten, setelah konvergensi, jika hasilnya tidak baik, maka oke, kernel linear yang kami gunakan tidak cukup baik karena data mungkin tidak linear, gunakan kernel yang berbentuk berbeda, coba kernel berbentuk berbeda jika Anda memiliki firasat, jika masih tidak, biarkan saja, itu adalah keterbatasan SVM.

Apa yang saya katakan adalah, jaringan saraf menjadi sangat tidak konsisten, bahkan tidak salah! Ia tidak pernah menerima kekalahannya! Insinyur / desainer menanggung beban, seandainya tidak bekerja seperti yang diinginkan.